2020-03-01

B树和B+树 - 上

1. 磁盘结构与数据存储

B树是针对磁盘专门设计的一种数据结构，所以我们先看下磁盘的结构，图1展示了一个磁盘盘片的逻辑划分，盘片被分成许多扇形的区域，每个区域叫一个扇区。以盘片中心为圆心，不同半径的同心圆称为磁道。扇区与磁道相交的部分成为块，因此可以根据扇区和磁道对块进行寻址，例如图中示例块的地址则是第2扇区、第2磁道。块是磁盘最小的逻辑单元，所以对磁盘进行读写操作也是对块的操作，通常块的大小为512字节（取决于各个厂商的实现），块内每个字节有自己的偏移位置如图2，因此只要知道扇区、磁道、偏移位置，就可以对磁盘某特定字节进行读、写操作。

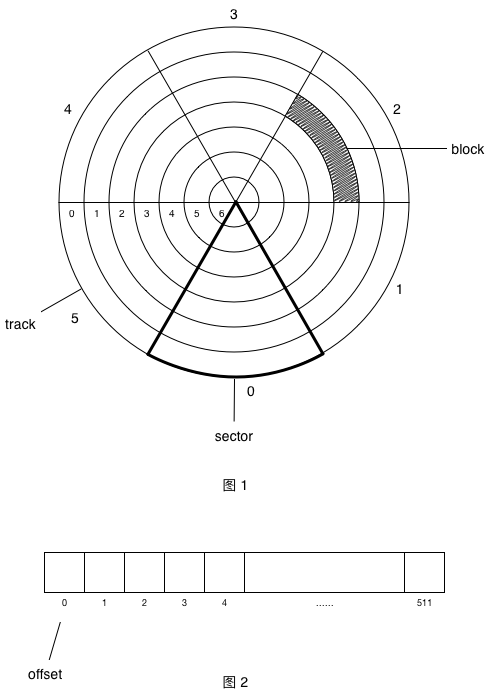
磁盘中的数据程序无法直接访问，因此程序需要先将磁盘上的数据加载内存中，待程序处理完后将结果写入到磁盘中。下面我们看下数据是如何存储在磁盘上的，我们这里有张员工信息表，表里存放有100条记录：

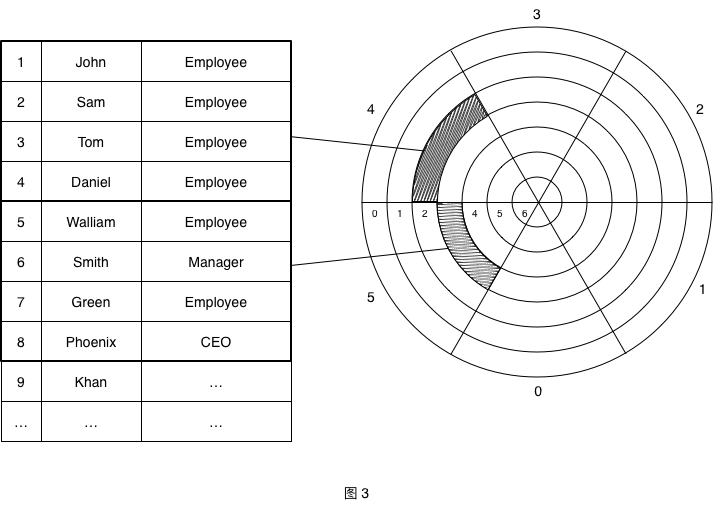
每个字段大小假定如下：cid 14字节，name 64字节、dept 50字节，那么一行记录则占用128字节，若一个块大小为512字节，那么一个块能存放的记录数则是：512 / 128 = 4 条记录。如图3所示，第1-4条记录存放在第4扇区、第2磁道上，第5-8条记录存放在第5扇区、第3磁道上。按照表中现有的100条记录计算，则需要占用磁盘的块数为：100 / 4 = 25 块。也就说如果我们现在要根据id或name去搜索员工信息需要遍历访问25个磁盘块，那么还有更快的方式可以访问到数据库中的数据吗？下面我们先介绍索引。

2. 索引和多级索引

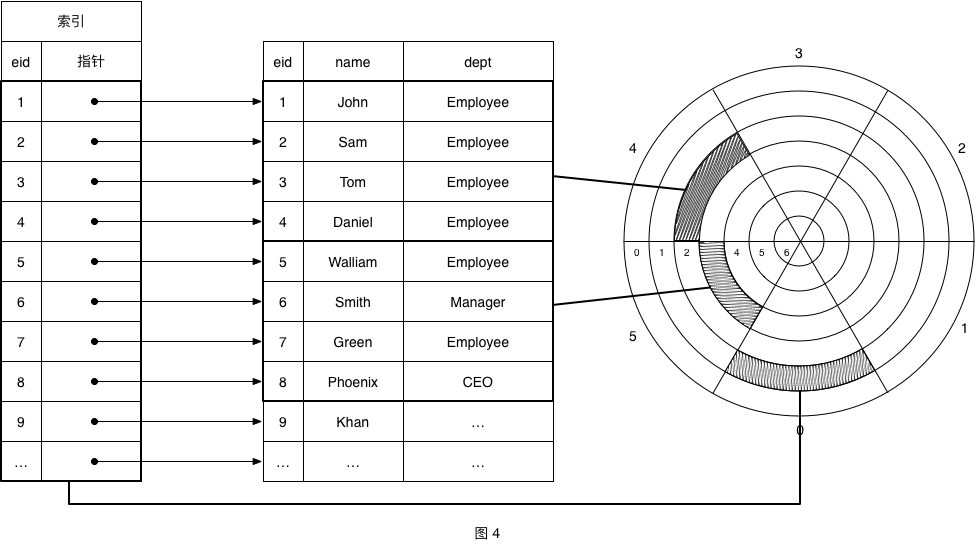
我们为数据库准备一个索引表，索引表中要存什么数据呢？我们将存储一个员工ID和一个指向该记录在磁盘所在位置的记录指针，那么索引表又该存在哪里呢？我们只能也将索引表存在磁盘上（所以一张表的大小包含数据部分大小+索引部分大小），那么索引要占用多少磁盘空间呢？让我们分析下：eid 10字节、记录指针 6字节，则每一条索引占用16字节，一个指定的磁盘块可以存储的索引记录数：512 / 16 = 32 条记录，则当前表总共索引占用磁盘块：⌈100 / 32⌉ = 4，此时搜索一条指定的记录，则先遍历索引获取记录指针后再根据记录指针访问磁盘，所以最多需要访问5个磁盘块即可找到记录，和刚没有索引时查找记录效率大大的提高了。现在我们表中只有100条记录，如果记录增加到1000条，那么数据需要占用250个块，索引需要占用32个块，随着数据的持续增加搜索索引本身也会非常耗时，那么此时是否可以在增加索引表的索引来加快数据访问？此时就引入多级索引。

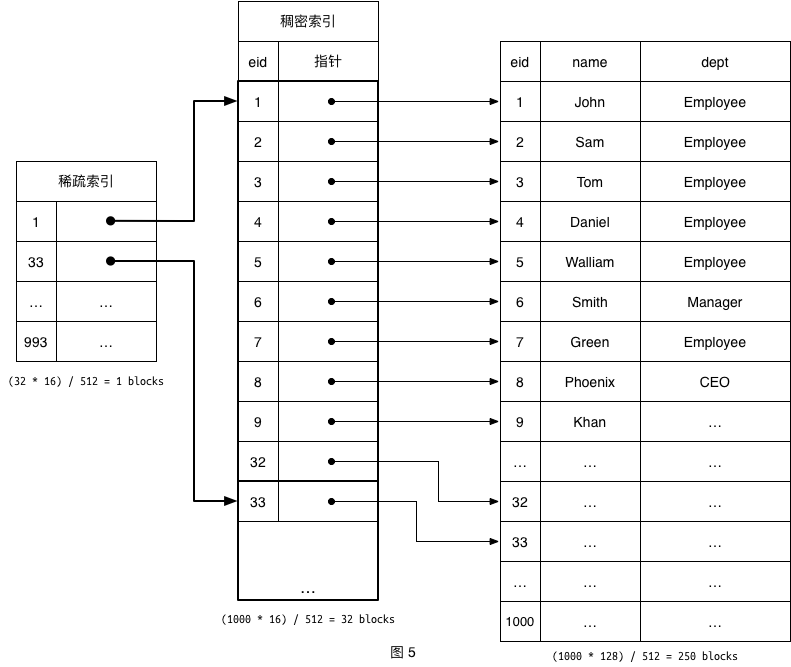
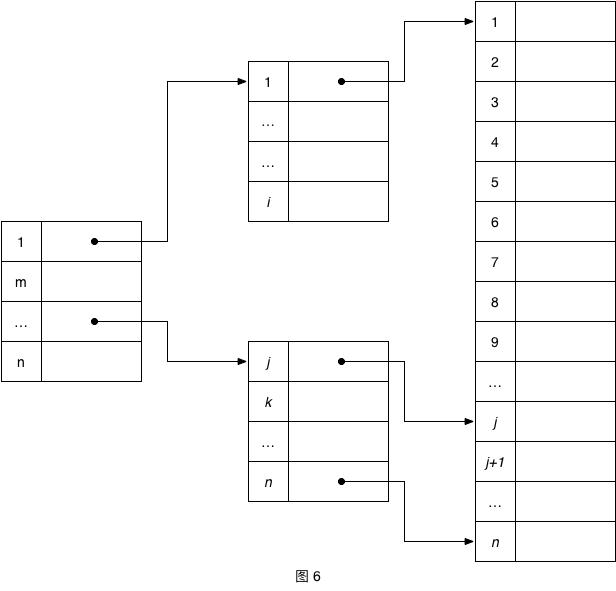
如上图所示建立了多级索引之后，一条多级索引记录的记录指针指向的是一个磁盘块的地址，1000条记录占用32个磁盘块，那么多级索引的存储仅占用1个磁盘块即可。此时再来查找则需要访问两次索引就可以拿到数据地址，再根据数据地址访问数据，3次磁盘访问就可以取到数据。如果顶级索引继续增加，那么再对其继续增加索引，如图6，此时如果将图中的结果旋转一下就得到一棵树型结构。在数据增加或减少的时候我们不可能手动去增加或删除索引，而是希望有一棵可以自我管理的结构，系统可以自动完成的树型结构，这就是B树/B+树的雏形。

3. 多路搜索树

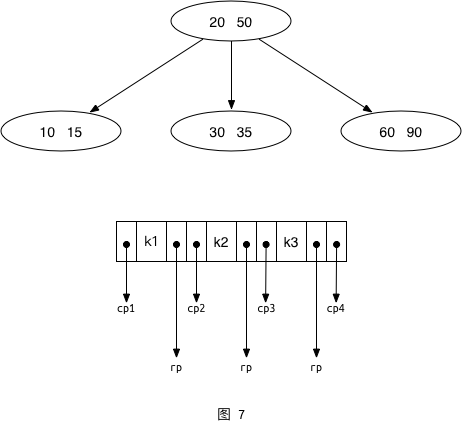
B树/B+树其实起源于多路搜索树（M-Way Search Tree），所以在介绍B树之前下面我们先看下多路搜索树。多路搜索树就是每个结点有M-1个元素，且每个结点有至多M个子结点。如下图所示的三路搜索树，每个结点有两个元素、最多有三个子结点。子结点的个数也就是结点的度，树的度就是所有结点中度的最大值。

4. B 树

B树本质是一棵平衡多路查找树，只不过多了一些规则，一棵B树T是具有如下性质的有根树（根为root[T]）：

每个结点x有一下域（字段）
1. n[x]，当前存储在结点x中的关键字数
2. n[x]个关键字本身，以非降序存放，因此 key₁[x] ≤ key₂[x] ≤ …key_n[x][x]
3. leaf[x]，是一个布尔值，如果x是叶子结点的话，则它为TRUE，如果x为一个内结点则它为FALSE
每个内结点x还包含n[x]+1个指向其子女的指针c₁[x]，c₂[x]，…，c_n[x]+1[x]，叶结点没有子女，故它们的c_[i]域无定义。
各个关键字key_i[x]对存储在各个子树中的关键字范围加以分隔：如果k_i为存储在c_i[x]为根的子树中的关键字，则：k₁ ≤ key₁[x] ≤ k₂ ≤ key₂[x] ≤ …key_n[x][x] ≤ k_n[x]+1
每个叶结点具有相同的深度，即树的高度h。
每一个结点能包含的关键字数有一个上界和下界。这些界可用一个称作B树的最小度数的固定整数t≥2来表示。
1. 每个非根的结点必须至少有t-1个关键字。每个非根的内结点至少有t个子女。如果树是非空的，则根结点至少有一个关键字。
2. 每个结点可以包含至多2t-1个关键字。所以一个内结点至多有2t个子女，我们说一个结点是满的，如果它恰好有2t-1个关键字。

t = 2时的B树是最简单的。这时每个内结点有2个、3个或4个子女，也就是一棵2-3-4树，不过在实际中，通常采用大得多的t值。

B树的插入自底向上进行的，具体操作插入操作如何进行，我们下次分析（挖坑先）。

5. B+ 树

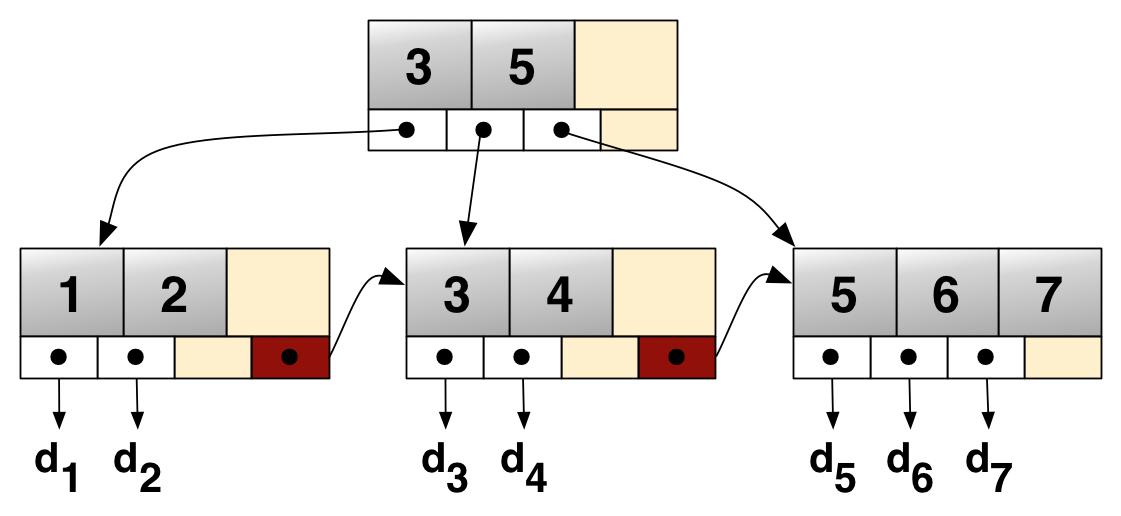
B+树的树定义和B树类似，不过有一些小的不同：B树内部结点有存储记录指针，B+树的内部结点不存储记录指针；所有的数据都存放叶子结点上，而且叶子结点是一个链表结构。B+树的一个最大的好处就是扫库非常方便，B树必须用中序遍历的方法按序扫库，而B+树直接遍历叶子结点即可，所以B+树支持范围查询非常方便，而B树没有这一特性，这也是数据库选用B+树的最主要原因。

6. 总结

本次主要从磁盘结构入手分析了数据、索引存放在磁盘中是如何组织的，进而分析了B树、B+树的为何要这样设计，最后分析了B+树作为数据库存放数据的优点。